English of course not only has ambiguity, but is all the richer for it. I’m sure there’s good evolutionary social science making the case for ambiguity being absolutely essential for the success of a language, but we all instinctively know why this is so. We all value occasionally not quite meaning what we say.
Latent Semantic Analysis
Sounding like a bad stomach bug Latent Semantic Analysis (LSA) is a technique to try and come to understanding from context. LSA starts by looking at the presence of words (and each document is seen as just a bags of words) in a document. When this happens across a bundle of different documents we see that some docs show higher representation for certain words, i.e. clustering occurs. This makes sense: chickens, pigs and sheep are much more likely to appear together and in docs from Farmers’ Weekly than say rates, credit, and reverse floaters (showing my age there!). It seems contradictory, but LSA’s starting point is to ignore context / meaning / word-ordering / ambiguity etc. altogether and simply count the presence of words. From counting, concepts are inferred by the presence of groups of words.
The Count Matrix
So we can think of LSA as presenting itself in two directions, words (vertical) and document reference (horizontal). There are a few modifications to the counting process (we get rid of stopwords – common words such as 'and', 'it', 'the'; uppercase, punctuation etc.) the most important of which is TFIDF. For any word we care about its Term Frequency (frequency of that term/word in any document) as a measure of its in-document relevance divided by (the Inverse bit) its Document Frequency (fraction of documents containing the term) so that terms frequently used across lots of documents become reduced in importance. (Log counting is used but that shouldn't trouble us here.)
A tall & slender Corpus (there's a reason it's not short and fat!)
In thinking about it, you will quickly come to realise that the y-axis tends to be very long: each author has the whole of the English language to choose from; each subsequent 'book' will have lots of overlap in word choice but also much heterogeneity, and accordingly we end up with something called a sparse matrix (lots of blanks / zeroes).
Into the Matrix: SVD
So, we’ve got this grid showing modified word counts (more accurately ‘frequencies’) by document. Now what? We will use Singular Value Decomposition to break it down. You can look up the details of SVD elsewhere, but in essence it breaks apart that grid. Today the grid captures two concepts/things at once (let’s call them ‘wordishness’ and ‘bookishness’ – bear with me, not as absurd as it sounds). SVD splits these so that we have two separate grids, one capturing ‘wordishness’ only (words down left; wordishness across top) and the other ‘bookishness’ only (books across top; bookishness down the left). When we multiply them together we perfectly (see below) recreate the original. Visually it looks a bit like this -
Sounding like a bad stomach bug Latent Semantic Analysis (LSA) is a technique to try and come to understanding from context. LSA starts by looking at the presence of words (and each document is seen as just a bags of words) in a document. When this happens across a bundle of different documents we see that some docs show higher representation for certain words, i.e. clustering occurs. This makes sense: chickens, pigs and sheep are much more likely to appear together and in docs from Farmers’ Weekly than say rates, credit, and reverse floaters (showing my age there!). It seems contradictory, but LSA’s starting point is to ignore context / meaning / word-ordering / ambiguity etc. altogether and simply count the presence of words. From counting, concepts are inferred by the presence of groups of words.
The Count Matrix
So we can think of LSA as presenting itself in two directions, words (vertical) and document reference (horizontal). There are a few modifications to the counting process (we get rid of stopwords – common words such as 'and', 'it', 'the'; uppercase, punctuation etc.) the most important of which is TFIDF. For any word we care about its Term Frequency (frequency of that term/word in any document) as a measure of its in-document relevance divided by (the Inverse bit) its Document Frequency (fraction of documents containing the term) so that terms frequently used across lots of documents become reduced in importance. (Log counting is used but that shouldn't trouble us here.)
A tall & slender Corpus (there's a reason it's not short and fat!)
In thinking about it, you will quickly come to realise that the y-axis tends to be very long: each author has the whole of the English language to choose from; each subsequent 'book' will have lots of overlap in word choice but also much heterogeneity, and accordingly we end up with something called a sparse matrix (lots of blanks / zeroes).
Into the Matrix: SVD
So, we’ve got this grid showing modified word counts (more accurately ‘frequencies’) by document. Now what? We will use Singular Value Decomposition to break it down. You can look up the details of SVD elsewhere, but in essence it breaks apart that grid. Today the grid captures two concepts/things at once (let’s call them ‘wordishness’ and ‘bookishness’ – bear with me, not as absurd as it sounds). SVD splits these so that we have two separate grids, one capturing ‘wordishness’ only (words down left; wordishness across top) and the other ‘bookishness’ only (books across top; bookishness down the left). When we multiply them together we perfectly (see below) recreate the original. Visually it looks a bit like this -
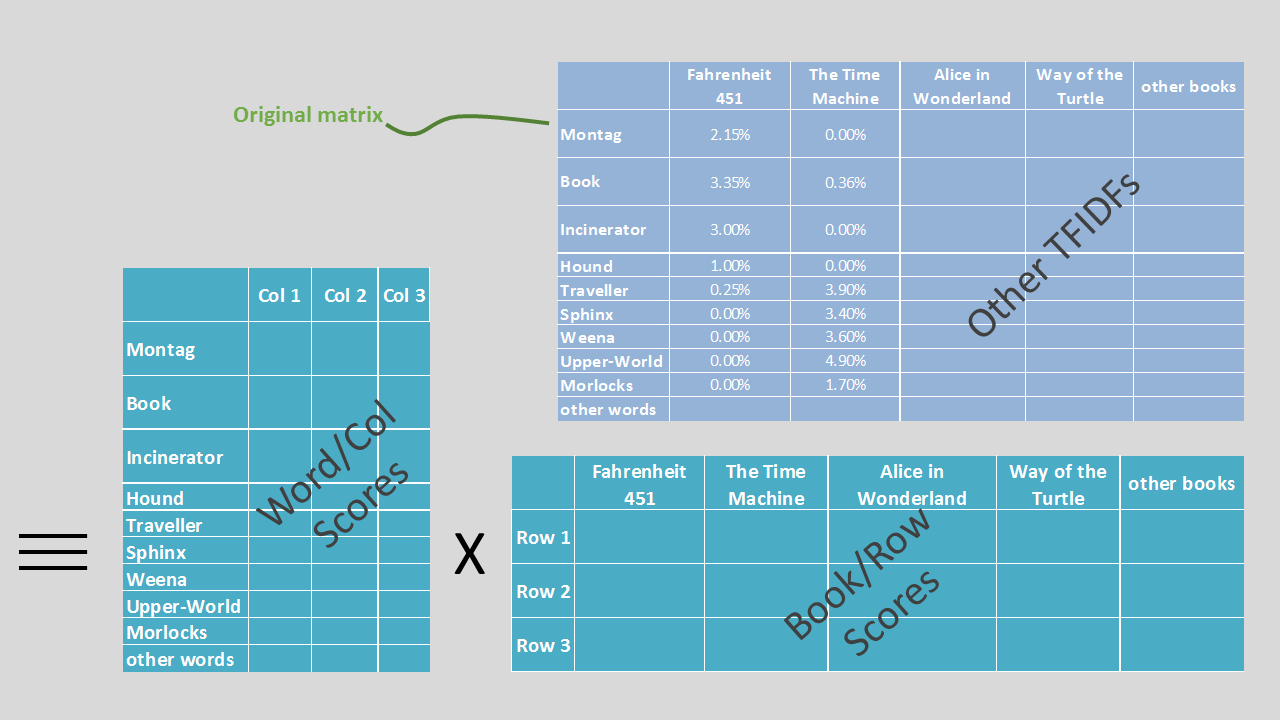
A bit more detail
The mechanics of matrix maths means a third grid gets slotted in-between these two, but it just exists to unitise things (keeping column entries so they sum to 1). The proper terminology you see for my three elements – the wordy, unitiser and booky grid - is U s V (for the left, singular value and right vectors).
Perfect Reconstruction?
I said ‘perfectly’ above but that isn’t always entirely true (and really, what would be the point?). What we actually find is that the each of the columns of U (tall and thin) is in order of decreasing importance. That is, the first column captures most of the information we need to produce the word-book grid; the second a bit less and so on. Funnily enough, the same happens with the V matrix (short and wide) where each row decreases in importance. So the net effect of SVD is to reorder the signalling / important information toward the leftmost columns / uppermost rows and push the noise toward the right and bottom. And, in fact, the s matrix gives us a quantifiable measure of the decreasing importance of each column. In this way we can begin to think of these U columns and V rows as representing concept space. The U matrix tells us where our word sits within word-space, and the V matrix where our doc sits within doc-space.
Next Post
We'll follow this post up with a real code example, but we've gotten to where we want to today: seeing that without much more than counting (and understanding nothing about language per se) we can begin to improve upon bag-o-words models and see pattern and context within documents.
The mechanics of matrix maths means a third grid gets slotted in-between these two, but it just exists to unitise things (keeping column entries so they sum to 1). The proper terminology you see for my three elements – the wordy, unitiser and booky grid - is U s V (for the left, singular value and right vectors).
Perfect Reconstruction?
I said ‘perfectly’ above but that isn’t always entirely true (and really, what would be the point?). What we actually find is that the each of the columns of U (tall and thin) is in order of decreasing importance. That is, the first column captures most of the information we need to produce the word-book grid; the second a bit less and so on. Funnily enough, the same happens with the V matrix (short and wide) where each row decreases in importance. So the net effect of SVD is to reorder the signalling / important information toward the leftmost columns / uppermost rows and push the noise toward the right and bottom. And, in fact, the s matrix gives us a quantifiable measure of the decreasing importance of each column. In this way we can begin to think of these U columns and V rows as representing concept space. The U matrix tells us where our word sits within word-space, and the V matrix where our doc sits within doc-space.
Next Post
We'll follow this post up with a real code example, but we've gotten to where we want to today: seeing that without much more than counting (and understanding nothing about language per se) we can begin to improve upon bag-o-words models and see pattern and context within documents.